Appendix: Technical Issues Affecting the Accuracy Reporting Programme
Note: The hard copy version presented to the House of Representatives did not include this Appendix. It was added in the PDF version, and is reproduced here, for the interest of those concerned with technical issues of measurement affecting the Accuracy Reporting Programme. Addition of the Appendix has no implications for the findings, conclusions, and recommendations set out in the report.
- Introduction
- Sampling Error
- Measurement Reliability
- Non-Sampling Errors
- Accuracy of the 5+5 Checks
- Issues Associated with Combining ARP Data with Data from the 5+5 Checks of Case Managers’ Performance
- Sampling Issues
- References
Introduction
1.
The Accuracy Reporting Programme (ARP) used by the Ministry of Social Development (the Ministry) involves drawing a statistically random sample of benefits and checking each one for accuracy. Such individual checks are generally referred to by statisticians as observations (or sometimes as experiments or trials). For each observation in the ARP process, there are only two possible outcomes – the benefit was either correct or in error.
2.
When an observed variable21 can have one of two possible values, it is referred to as binomial. Suppose that the total number of all benefits is N, the true proportion of correct benefits is P, and the true proportion of errors is Q. If a sample of n observations are made, and an observed number c are correct, then the remaining observations e must all be errors, so that:
c + e = n
3.
The collected results of a number of binomial observations can also be expressed as proportions, so that:
c/n = p
e/n = q
p + q= 1
4.
There are at least three significant reasons why the observed proportions p and q might not be the true proportions P and Q. These are:
- sampling error;
- measurement reliability; and
- non-sampling errors.
In this appendix we will provide some explanation of these possible sources of error and how two of them can be quantified.
Sampling Error
5.
Since its value is derived from random sampling, it is not likely, except by lucky accident, that the observed proportion p of correct benefits in the sample will exactly equal the true proportion P of correct benefits in the total “population” of all benefits (and likewise, that the sample proportion q will exactly equal the true proportion Q).
6.
For example, we might choose a sample n of 1000 benefits from a total population N of 1,000,000 benefits. The true proportion P of correct benefits in the total population might be 0.9 (that is, 90%) and the true proportion of errors (Q) might be 0.10 (10%). However, because it is chosen at random, our particular sample of 1000 benefits might disclose a sample proportion p of correct benefits of 0.87 (87%) and a sample proportion q of errors of 0.13 (13%).
7.
Given that the proportions observed from a sample are not likely to be exactly the same as the true proportions, it would be very useful to have some idea of how far the observed values are likely to differ from the true values.
8.
Intuitively, we might realise that if the sample size n is very large in relation to the population size N, the observed values of p and q are likely to be very close to P and Q (because, if the sample size n was actually equal to N – and assuming that our observations were always accurate – by definition, p would exactly equal P and q would exactly equal Q). Similarly, if n is very small in relation to N then the chances of a significant difference between p and P (and between q and Q) are much higher. The bigger the sample, the more likely the estimate is to be accurate. But how much more likely?
9.
Statisticians have devised a useful method for assessing how likely it is that p is a good estimate of P. The method is known as a confidence interval.
10.
A confidence interval is a span of possible values of P. It can be calculated by a formula that has been devised to ensure that, in a given high percentage of cases, the interval will include the true value P. In the example already cited, if an observed value is 0.87, some confidence interval might be a span of possible values of P that ranged from 0.82 to 0.92 (which, in this example, does indeed contain the true value of P, namely 0.90).
11.
To better explain the concept of a confidence interval, we need to develop the previous example further. From our particular sample of 1000 benefits, we obtained observed proportions p = 0.87 and q = 0.13. If we had drawn some other random sample of the same size, we might have obtained a slightly different pair of observed values – say, p = 0.89 and q = 0.11. If we drew a third sample of the same size, we might have obtained yet another set of observed values – say, p = 0.91 and q = 0.09. (Remember that the true values in this example are P = 0.90 and Q = 0.10.) If we took numerous samples of 1000 benefits, we would expect to find our observed values of p and q clustered around the true values P and Q. If we took very many such samples, we would expect to find most observed values of p and q were quite close to P and Q, and only a few observed values of p and q which were significantly different from P and Q (because in those few cases we happened to draw a quirky sample).
12.
Because:
- each observed value of p is particular to the actual sample from which it was observed; and
- each observed value of p will in general be slightly different from the values of p observed from other samples;
the confidence interval calculated from a particular sample will in general be slightly different from the intervals calculated in the same way but using the observed values from other samples. However, we can decide in advance how sure we want to be that the span of our confidence interval will be wide enough to contain the true value P. We can then calculate a confidence interval of the appropriate width.
13.
For example, if we specify a 95% confidence interval, we can calculate a span of possible values of p that, in 95% of cases, will include the true value of P. In other words, given a total population of N, if we had drawn all the very many possible samples of size n and calculated confidence intervals for all the observed values of p, 95% of those confidence intervals would contain the true value P.
14.
There is no particular reason why we should have chosen 95% (although that is a commonly-used figure). We could have chosen some other percentage – for example, 90% if we didn’t need to be quite so sure that the interval contained the true value, or 99% if we needed to be very sure that the interval contained the true value.
15.
A number of methods have been devised for calculating the confidence interval of a proportion and there has been considerable technical debate about the best method. Computer simulations have shown that all methods have some flaws, including the so-called “exact” methods. (These have also been shown not to be exact at all, but conservative approximations.) The precise extent of the discrepancies associated with each method varies, depending on the values of p and n. However, if the sample size is reasonably large, most methods will produce very similar confidence intervals. The difficulties come when the sample size is small and the observed proportions are very low or very high.
16.
The most commonly used method for calculating a 95% confidence interval for an observed proportion was devised by Abraham Wald. It applies the following formula:
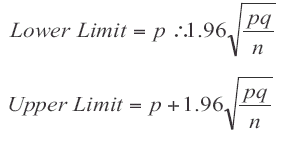
17.
However, there are some difficulties with the Wald method. For example, it does not work at all without modification in cases where:
- the formula produces a limit for the confidence interval that is less that 0 or greater that 1 (implying a negative proportion or a proportion greater than 100%, both impossible); or
- the observed proportion is zero.
18.
Most textbooks on statistics teach the Wald method and assert that it is an acceptable method if the sample size n is reasonably large and p is not too close either to 0 or 1. However, recent research (for example, Brown, Cai and Das Gupta, 2001) has shown it to be much more erratic across wider ranges of p and n than had previously been understood.
19.
Agresti and Coull (1998) devised a method they term the “modified Wald” method. It is computationally similar to the Wald method but uses simple adjustments to the values of p, q and n. Computer simulations have shown it to be more accurate in most circumstances than other methods, including the so-called “exact” methods. It is the method recommended by Brown, Cai and DasGupta for cases where n ≥ 30 and accordingly we have adopted it for use in this study.
20.
The necessary modifications for a 95% confidence interval are:
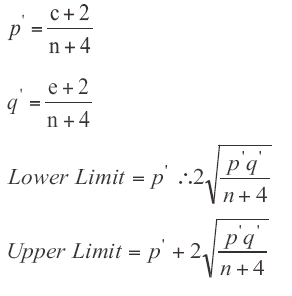
21.
If the lower limit calculated using that equation is less than 0, set the lower limit to 0. Similarly, if the upper limit is greater than 1, set the upper limit to 1.
22.
For any values of p and n, at least 92% – and generally around 95% – of intervals calculated by using this formula will contain the true result. It also deals more effectively with cases where the observed proportion p is 0.
23.
It is possible to use confidence intervals to make judgements about whether or not it is safe to assume that the error proportions in two separate populations of benefits are actually different. For example, if the ARP-determined level of benefit accuracy in any given year is 91% and in the next year is 90%, are we safe in concluding that the level of benefit accuracy has actually declined from the previous year?
24.
The simple rule is that if the confidence intervals do not overlap, it is safe at the given level of confidence to conclude that the true proportions are indeed different. However, if two confidence intervals overlap, the difference between the observed proportions might or might not be statistically significant – without further scrutiny it is unsafe at that level of confidence to conclude that the true proportions are actually different.22

25.
To return to the example just cited, the 95% confidence interval for the national ARP measure of benefit accuracy is approximately ± 1%. The 95% confidence interval for the first year is therefore 90% – 92% and for the second year is 89% – 91%. Since these confidence intervals overlap (across the range 90% – 91%), it is unsafe to conclude at the 95% level of confidence that accuracy levels have in fact declined. However, if the ARP measure for the second year was 88%, (and the confidence interval was therefore 87% – 89%), it would be safe at the 95% level of confidence to conclude that accuracy levels had actually declined.
Measurement Reliability
26.
In measurement theory, there are several ways of defining and interpreting the concept of the reliability of a method of measurement23. For most practical purposes, however, the concept is motivated by a simple question – If we measure a particular item again using the same method of measurement, how likely are we to get the same result?
27.
For example, repeatedly measuring a particular length of wood with a well-calibrated wooden ruler might produce highly consistent results. In such situations, the measurement is said to be reliable. However, repeatedly measuring the same length of wood with a tape measure made from elastic might produce highly inconsistent results, because small changes in tension may cause significant stretching or contracting of the tape. In such situations, the measure is not reliable. Most methods of measurement are unreliable to some extent, and it is useful to have some idea of how reliable or unreliable they actually are.
28.
In relation to the ARP, the most likely reason that the observed value p will differ from the true value P (apart from sampling error) is measurement error. For each observation made (i.e. each benefit sampled), an assessor makes a judgement about whether or not the benefit is correct. But the assessor’s judgement may itself be wrong. In reporting ARP measurements of benefit accuracy, it would be useful to present some idea of how likely it is that some of the assessors’ judgements were wrong.
29.
It seems to us that there are two possible approaches.
- estimating and reporting the standard error of measurement; and
- estimating and reporting inter-assessor reliability.
30.
The concept of a standard error of measurement is derived from a set of assumptions and consequential deductions that are known as “true score theory” (TST). Among other assumptions, TST assumes that a measurement has a “true” score and that actual measurement errors are normally distributed24 around the true score. The span of possible values for the true score that is one standard deviation wide is known as the standard error of measurement.
31.
It is rare that a large number of repeated measurements of a particular value have been made, so that the standard deviation of the measurement error distribution can be estimated directly. However, by making the further assumption that the measurement error distributions of all measurements in a particular sample are the same, it is possible to estimate the standard deviation of that common distribution from the observed correlation between single repeat measurements of each observation in the sample.
32.
The standard error of measurement is a commonly-used metric of reliability, but it is sensitive to a number of assumptions. On balance, we don’t favour its use in ARP reporting.
33.
A second approach is to measure the inter-assessor reliability25. This can be done by having a number of assessments rechecked by an independent second assessor (who should be unaware of the original assessment). The inter-assessor reliability can then be determined by calculating the correlation between assessors’ judgements. A highly correlated set of judgements implies a high degree of reliability in the observed levels, while a weakly correlated set of judgements implies that the observed levels of benefit accuracy will be somewhat uncertain.
34.
We consider that reporting inter-assessor reliability would constitute a useful enhancement of the ARP, and we recommend its introduction.
Non-Sampling Errors26
35.
ARP accuracy figures, even at national level, make no allowance for non-sampling errors, measurement errors, or any other possible types of errors that may be related to misapplied technical methods, for example. We are unaware of any study or report by the Ministry on such matters. However almost no survey can escape at least some non-sampling errors. We therefore recommended that a study be undertaken by the Ministry to assess the extent of such problems, and a report prepared.
36.
Non-sampling errors can take a very wide variety of forms. See for example Lesser et. al., 1992. Finding non-sampling errors, assessing their importance, and dealing with them in detail, would require considerable interaction with staff of the Ministry, and is consequently beyond the scope of this report.
Technical Issues Affecting the 5+5 Checks of Case Managers’ Performance
Accuracy of the 5+5 Checks
37.
The 5+5 procedure itself, as applied once only to individual staff, uses sample sizes that are too small to provide a satisfactory measure of individual staff performance. To illustrate, consider a staff member who meets a 90% accuracy (i.e. 10% error) requirement in terms of errors made in cases/files for which s/he is responsible. Then (ignoring the equivalent of finite populations corrections for simplicity, and under simple random sampling) the probabilities that this staff member has 0, 1, 2, 3, 4, 5 errors found in five sampled files are given by:
| Number of errors in sample of size 5+5=10 | |
Probability given real error rate meets 10% standard |
|---|---|---|
| 0 | (0.9)5 = | 0.59049 |
| 1 | 5*(0.1)*(0.9)4 = | 0.32805 |
| 2 | ((5*4)/2)*(0.1)2*(0.9)3 = | 0.07290 |
| 3 | ((5*4)/2)*(0.1)3*(0.9)2 = | 0.00810 |
| 4 | 5*(0.1)4*(0.9) = | 0.00045 |
| 5 | (0.1)5 = | 0.00001 |
38.
Hence, the probability of finding two or more errors in a sample of size five, when the staff member actually meets a 90% error-free standard, is nearly 0.1 (which would penalise one such staff member in every 10), and the probability that the sample error rate is higher than the actual error rate is more than 0.4. This analysis ignores any incorrect assessments of whether a file is ‘in error’, but this fact does not allow the central problem (detailed below) to be avoided.
39.
The complication is that if a staff member’s actual error rate was unacceptable, say only 75% of his/her files were accurate, then the probability that this remains undetected by a sample of five of his/her cases can be derived as follows:
| Number of errors in sample of size 5+5=10 | |
Probability given real error rate meets 25% standard |
|---|---|---|
| 0 | (0.75)5 = | 0.23730 |
| 1 | 5*(0.25)*(0.75)4 = | 0.39551 |
| 2 | ((5*4)/2)*(0.25)2*(0.75)3 = | 0.26367 |
| 3 | ((5*4)/2)*(0.25)3*(0.75)2 = | 0.08789 |
| 4 | 5*(0.25)4*(0.75) = | 0.01465 |
| 5 | (0.25)5 = | 0.00098 |
40.
Hence, if zero or one error in the sample is acceptable (as from the previous analysis it certainly needs to be for good staff not to be incorrectly penalised more than one time in 10), then a staff member with an unacceptable error rate of one error in every four files has a considerably better than even chance (i.e. a probability of 0.23730+0.39551=0.63281 of going completely undetected.
41.
While the situation is rather better if all 5+5=10 files are considered together (see below), there remains a strong possibility that, when using a standard that does not penalise good staff too frequently, the errors of others go substantially undetected. This is clearly undesirable.
42.
In principle, an improved procedure would be to use some form of sequential sampling, where, if an unacceptable sample error level is found for a given staff member, a further sample is taken. This procedure would certainly require specialist advice to design and analyse, however, because the usual binomial or other tabulated probabilities (such as those above) are not conditional probabilities which are required at any additional phase of sampling, and so specialised calculations (and software programs) would be needed for implementation.
43.
However, it is very clear from this analysis that the present 5+5 scheme needs modification and larger sample sizes, if it is not to be rather arbitrary in its assessment of individual staff standards, at least when applied for a single period.
44.
If the 5+5 samples are treated as a single sample of size 10, it is instructive to consider the probability of finding a particular number of errors in the sample for a particular case manager, under two different scenarios:
- given the case manager’s work actually meets a 10% error standard,
- given the case manager’s work really has 25% of benefit files in error.
| Number of errors in sample of size 5+5=10 | |
Probability when actual error rate meets 10% standard |
|---|---|---|
| 0 | (0.9)10 = | 0.34868 |
| 1 | 10*(0.1)*(0.9)9 = | 0.38742 |
| 2 | ((10*9)/2)*(0.1)2*(0.9)8 = | 0.19371 |
| 3 | ((10*9*8)/(3*2))*(0.1)3*(0.9)7 = | 0.05740 |
| 4 | (10*9*8*7)/(4*3*2)*(0.1)4*(0.9)6 = | 0.01116 |
| Number of errors in sample of size 5+5=10 | |
Probability given real error rate is 25% |
|---|---|---|
| 0 | (0.75)10 = | 0.05631 |
| 1 | 10*(0.25)*(0.75)9 = | 0.18771 |
| 2 | ((10*9)/2)*(0.25)2*(0.75)8 = | 0.28157 |
| 3 | ((10*9*8)/(3*2))*(0.25)3*(0.75)7 = | 0.25028 |
| 4 | (10*9*8*7)/(4*3*2)*(0.25)4*(0.75)6 = | 0.14600 |
45.
Hence, if three or fewer errors in the sample of 10 is used as the criterion for acceptability, for example, then the chance of misjudging a staff member who actually meets a 10% error rate standard is about 0.07, i.e. about 1 in 14 such staff members would be wrongly judged as having unacceptable error rates. At this same standard however, a staff member whose error rate was 25% (i.e. 2.5 times higher than the 10% limit) would have a probability of 0.526 (i.e. a better than even chance) of not being detected (i.e. less than half the staff with a 25% error rate will be detected).
46.
The statistical conclusion is that a single 5+5 sample is too small to provide a fair assessment of case managers’ benefit file error rates, even if all 10 benefit files are combined for each case manager rather than treated as two separate groups of five. The problem is that the ‘statistical power’ of the test is low because sample sizes are too small.
47.
A situation which is not as imprecise is when a case manager’s 5+5 assessments are aggregated over a period. Because the period, and hence the number of assessments, may vary, further detailed analysis that meets all circumstances is not possible. However, the general methodology above will yield the numerical answers when it is used in combination with the relevant data.
Issues Associated with Combining ARP Data with Data from the 5+5 Checks of Case Managers’ Performance
48.
How can ARP and 5+5 sampling systems best be linked? One method involves what is called ‘double sampling’. A fundamental reference is Cochran (1977), especially Chapter 12, pages 327-358. Extension of these methods to the sampling schemes used for ARP and 5+5 sampling (at least within regional offices) would be necessary before implementation.
49.
How double sampling works can be illustrated with a simple biological example. Consider the problem of accurately measuring the surface area of all the leaves on a deciduous tree. Measuring the surface area of every leaf is not feasible. However, if a comparatively small number of leaves are taken, the surface area and dry weight determined for each, and the (regression) relationship between surface area and dry weight is estimated, all that is necessary after finding this relationship is to wait for all the leaves to fall, dry and weigh them. The regression relationship can then be used to estimate surface area from weight. This method is comparatively inexpensive.
50.
A parallel double sampling scheme for assessing error rates in the Ministry’s benefit files would be to use the relationship between 5+5 results and ARP results applied to a comparatively small sample of the same files, as the basis for combining all 5+5 results with the ARP results, to get more accurate benefit file error rate assessments. A sub-sample assessed by both methods would be used for calibration.
51.
If the Ministry was to adopt double sampling, further external technical input is highly recommended, particularly since the current sampling schemes for 5+5 and ARP differ. Detailing the required survey design for double sampling is beyond the scope of this report. However, the method looks promising and we recommend that it be investigated further.
Sampling Issues
52.
In this report, confidence intervals have been calculated on the assumption that sampling, including sampling within regions, is conducted in such a manner as will achieve a “simple random sample” (srs).
53.
It is not completely clear whether sampling within regions is on an srs basis. If sampling within regions is not by srs, it will have some effect on confidence intervals, although the effect should be slight for any common, easily implemented sampling scheme in the absence of marked sample clustering and any non-sampling problems.
54.
ARP sampling on a national basis uses stratified sampling by regional offices with proportional allocation for each office, based on the distribution of applications and reviews for the financial year 1995-96. The Ministry has stated that the variation in Applications and Reviews is not significant over time. This sampling scheme is not quite equivalent to an srs, although differences in estimated size of a confidence interval should be slight, so that the srs formula for a national confidence interval can be used as an approximation (given similarity of assessments of benefit assessment accuracy across offices) provided sampling within offices is by srs.
References
Agresti, A. and Coull, B. (1998). Approximate is Better than “Exact” for Interval Estimation of Binomial Proportions, The American Statistician, 52: 119–126.
Allen, M.J. and Yen, W. M., Introduction to Measurement Theory, Brooks Cole, 1979.
Brown, L.D., Cai, T.T. and Das Gupta, A., Interval Estimation for a Binomial Proportion, Statistical Science, 16, 2: 101–133.
Cochran, W.G., Sampling Techniques, 3rd Edition, John Wiley and Sons, 1977.
Haslett, S and Telfar, G., Sample Designs for Auditing Error Data: A Case Study, New Zealand Statistician, June 1995, Vol. 30, No. 1, pp 23–36.
Lesser, J.T. and Kalsbeek, W.D. Nonsampling Error in Surveys, John Wiley and Sons, 1992.
21: A common form of notation used in statistical literature is that a population parameter is denoted by an unembellished variable such as “p” and an estimate of that parameter obtained from a sample of the population is denoted by adding a circumflex “^” over the “p”. We have not used the common notation in this explanation in the belief that readers unfamiliar with mathematical notation often find it confusing until they have had time to become familiar with it.
22: Another approach is to calculate a confidence interval for the difference between the two proportions rather than calculating confidence intervals for each proportion separately.
23: A more detailed treatment is beyond the scope of this appendix. More information can be obtained from any text book on measurement theory – for example, Allen, M. J. and Yen, W. M., Introduction to Measurement Theory, Brooks Cole, 1979.
24: That is, distributed in accordance with the bell-shaped “normal” frequency distribution.
25: Also commonly known as “inter-rater agreement”.
26: The remainder of the analysis and associated conclusions in this appendix were provided by our technical referee, Professor Stephen Haslett.
page top